Начинаем разметку от первой стены
Первым делом проверим нашу первую стену на вертикаль и плоскость. Если выравниваем 2 угла, то это стена, параллельная ванне, если выравниваем 4 угла (всю площадь), то стена с проёмом. Если стена завалена, её нужно будет выровнять первым делом, но не торопитесь, ведь мы ещё не проверили всю площадь.
Для начала просто отобьём ровную линию параллельно первой стене, максимально приближённую к ней.
Проведём первую линию, параллельно первой стены
Далее между первой стеной и второй стеной установим угольник одной гранью параллельно первой линии, а на вторую грань угольника накладываем прави́ло. Совмещаем грань прави́ла и угольника, тем самым «удлинняя» наш угольник. Чертим линию на полу до конца стены максимально приближённую к стене. Регулируем и совмещаем наш увеличенный угольник так что бы:
- линия была ровной,
- расстояние до стены минимальным,
- вторая грань угольника была параллельна первой линии.
Так получаем первый прямой угол.
От первой линии отобьём вторую, перпендикулярную ей
Далее идём на следующий угол, до которого мы чертили линию, и совмещаем угольник одной гранью параллельно второй линии. Повторяем процедуру с правилом (совмещаем его с угольником) и чертим третью линию перпендикулярную второй, опять же максимально приближённую к стене.
Тут требуется некоторая сноровка, чтобы совмещать прави́ло, угольник и делать прямой угол с линиями, максимально приближёнными к стене (это делается для того, что бы при штукатурке «не съесть» лишнее пространство). Если прави́ла не хватает, дочерчиваем до куда хватает, переставляем прави́ло, совмещая его с линией, и проводим её до конца стены.
Чертим третью линию перпендикулярную второй
Чертим четвёртую линию, по аналогии. В итоге у нас должен получится начерченный на полу прямоугольник
внутри нашего помещения. Проверяем его по первой грани — по стене с проёмом, так же, прикладывая угольник и правило.
Проверяем по 1-й грани полученный прямоугольник
Если всё ровно, можно немного расслабиться. Если нет, повторяем процедуру и/или смотрим где ошиблись.
Прутик за прутиком
Опоры готовы. Можно начинать плетение. Первый прут положите, прижимая его конец к внутренней стороне кола, обогните следующий кол с внешней стороны, затем заведите его внутрь и так далее. Конец прута должен быть заправлен внутрь будущей корзины (лишнее обрежьте секатором). Следующие прутья до самого верха корзины заплетайте по такому же принципу. Время от времени (примерно через 30–40 см) плетения надо осаживать прутья, чтобы они ложились более плотно. Для этого плетение уплотняют ногой или с помощью кувалды.
Когда корзина будет закончена, выстелите ее стенки изнутри рубероидом. Сверху аккуратно прикрепите его в нескольких местах к кольям-опорам проволокой, а на дне присыпьте 10-сантиметровым слоем земли.
Индивидуальное значение
Тату «треугольник» для каждого человека является чем-то особенным
Так, например, для девушек эта простая на вид фигура, может означать кое-что важное и глубокомысленное. Треугольник – отображение трех циклов жизни практически любой женщины
Это девичество, материнство и старость. Не все могут додуматься до такого. Однако подобное разъяснение существует уже давно, и многие набивают треугольник намеренно с этой целью.
Для мужчин же фигура означает кое-что другое. Треугольник также символизирует «троицу», однако в данном случае это не цикл жизни, а качества. Если быть точнее, то мудрость, сила и красота
К слову, очень важно, какой был выбран участок для татуировки. Он способен усилить, подчеркнуть придаваемый смысл
Чаще всего такие тату можно видеть на запястье, предплечье или на затылке. Это самые популярные варианты исполнения. Но на самом деле человек сам выбирает место.
Иногда треугольники закрашивают. Цвет также означает очень многое. Красный символизирует страсть, черный – негатив, зеленый – безопасность, оранжевый – жизнелюбие. Оттенок действительно может рассказать о многом, так что выбирать его нужно особенно тщательно. И, кстати, стоит учитывать, что на коже выбранный цвет всегда смотрится на 2-3 тона темнее. Следует об этом знать и подбирать краску с осознанием данного факта.
Какие существуют альтернативные варианты
Как создать прямой угол
Лучшим вариантом смастерить прямой угол
является применение угольника или транспортира. Это позволит с минимальными затратами найти необходимые пропорции. Но, основной момент египетского треугольника в его универсальности из-за возможности создать фигуру, не имея под рукой ничего.
В этом деле может пригодиться все, даже печатные издания. Любая книга или даже журнал имеют всегда соотношение сторон, образующее прямой угол. Типографские станки работают всегда точно, чтобы рулон, заправленный в машину резался пропорциональными углами.
Древние инженеры придумывали много способов строительства египетского треугольника и всегда экономили ресурсы.
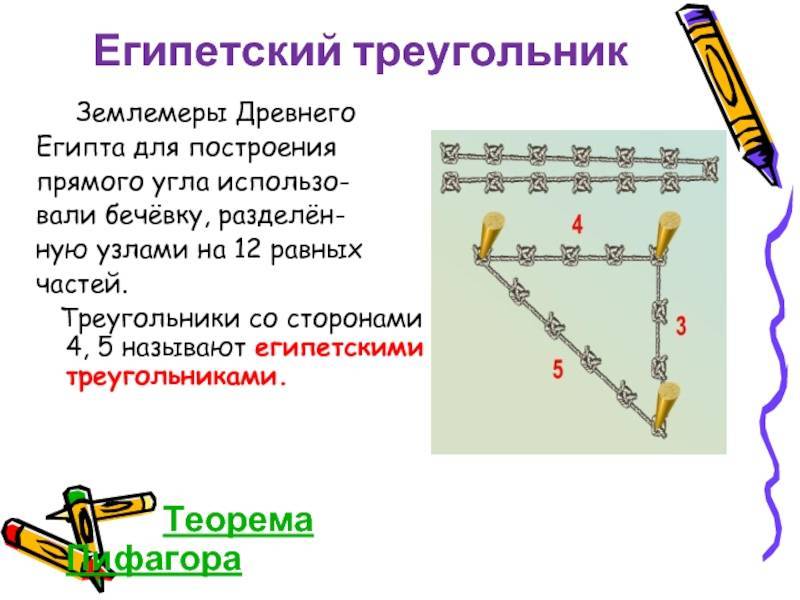
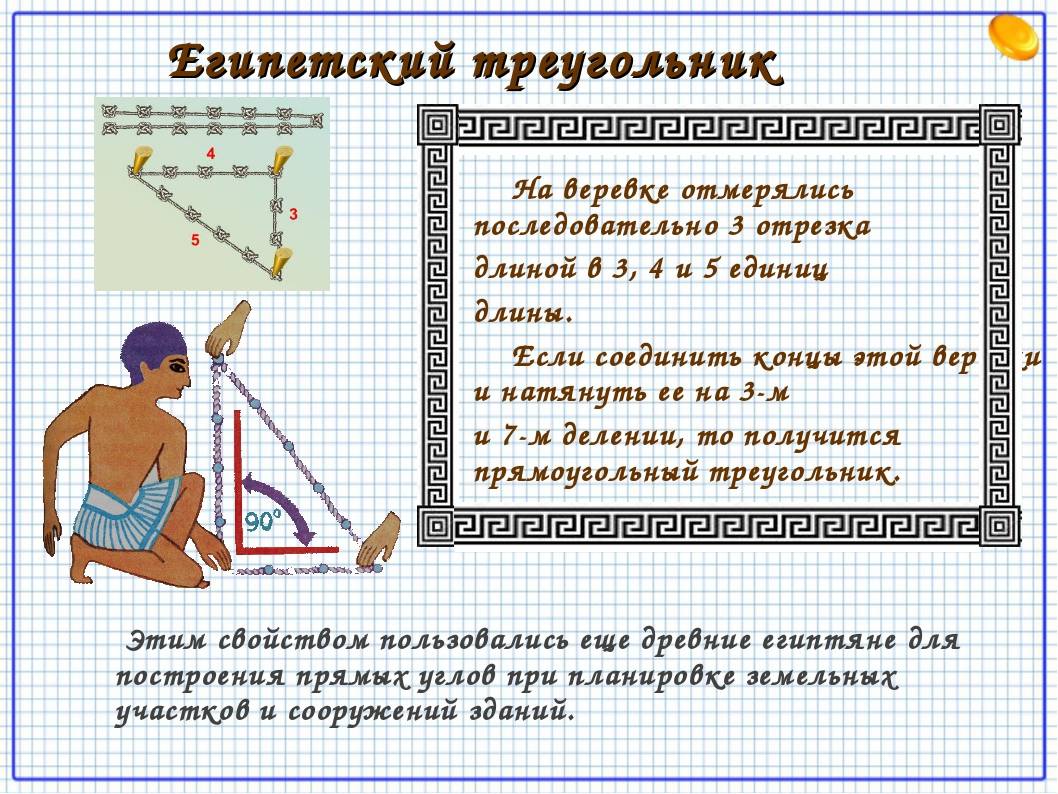
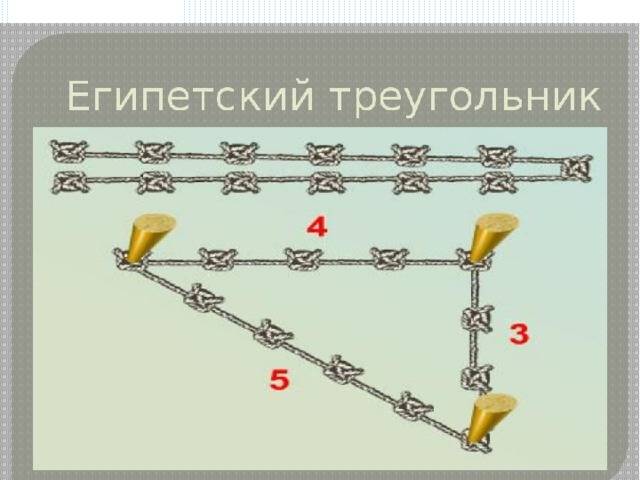
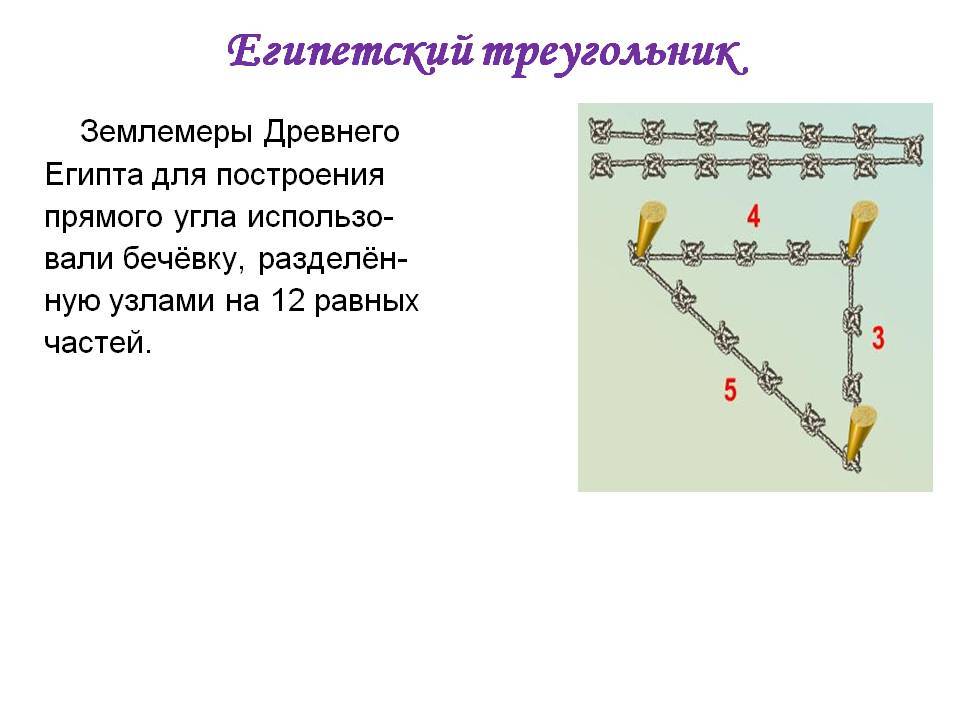
Поэтому, самым простым и широко применяемым был метод постройки геометрической фигуры с применением обычной веревки. Бралась бечевка и резалась на 12 ровных частей, из которых выкладывалась фигура с пропорциями 3,4 и 5.
Как создать другие углы?
Египетский треугольник в строительном мире нельзя недооценивать. Его свойства однозначно полезны, но без возможности построить углы другого градуса в строительстве невозможно. Чтобы образовался угол в 45 градусов, понадобится рамка или багет, которые распиливаются под углом в 45 градусов и соединяются между собой.
Глаз в треугольнике
Символ, графически представляющий собой вписанный в треугольник глаз, называемый «глазом провидения» или «всевидящим оком», появился в Европе в XVII в. Считается, что он восходит к солярному глазу Гора древних египтян. Этот знак получил широкое распространение в барочной архитектуре, украшая фронтоны роскошных католических костелов.
В XIX в. он появился и на православных храмах, например, на фронтоне Казанского собора в Санкт-Петербурге. Христианство рассматривало его как символ Святой Троицы. Одновременно этот символ использовался и масонами, которые трактовали его как символ абсолюта, просвещения и высшего знания. У масонов «глаз провидения» располагается над стулом мастера ложи, чтобы таким образом напоминать о всепроникающей во все тайны мудрости Творца.

Декларация прав человека и гражданина, Франция, конец XVIII в.

Герб белорусского города Браслав
Доказательство
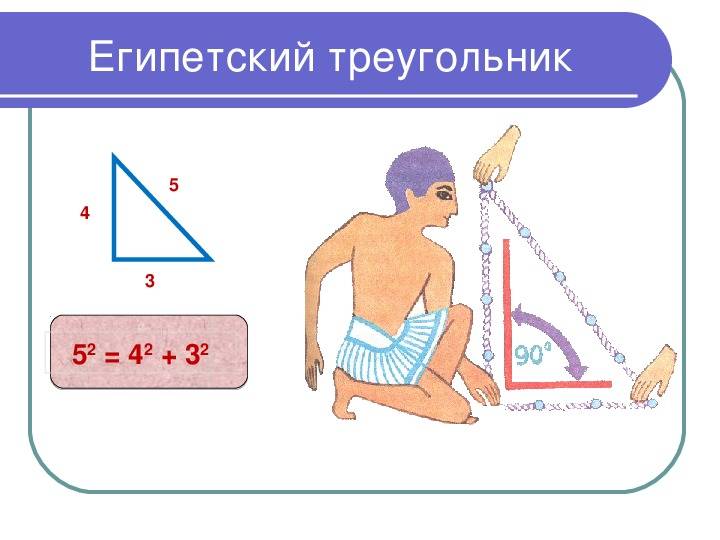
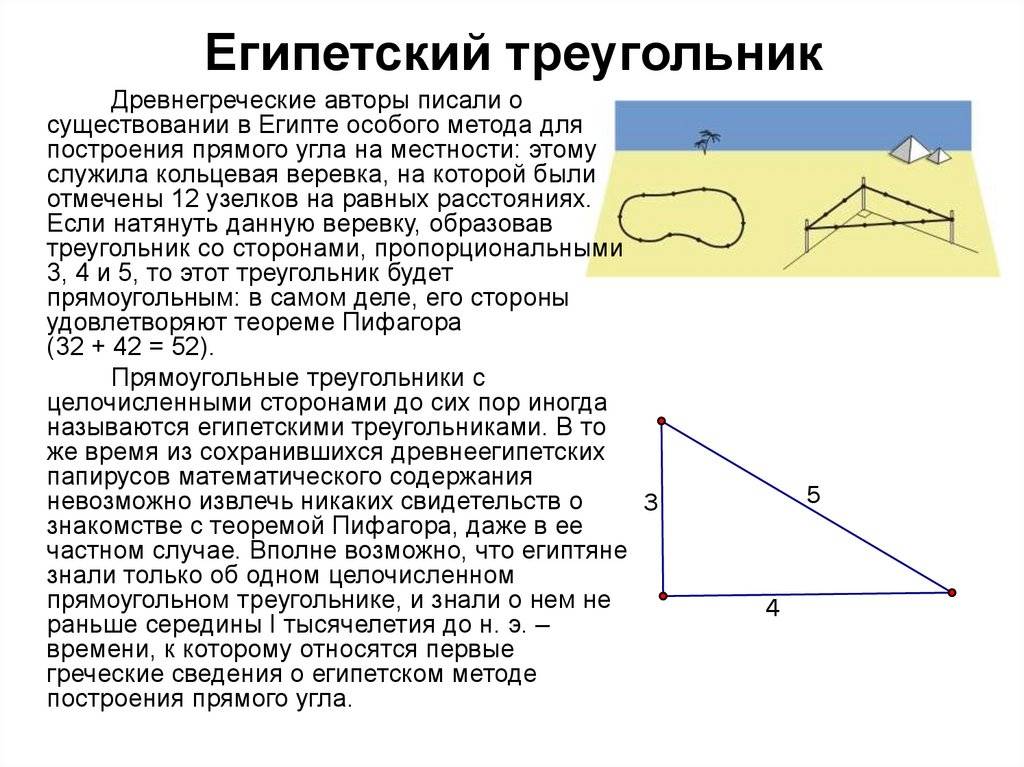
При помощи некоторых простых вычислений можно доказать, что треугольник является прямоугольным. Если следовать теореме обратной той, которую создал Пифагор, т. е. в случае, если сумма квадратов двух сторон будет равняться квадрату третьей, то он прямоугольный, а поскольку его стороны приводят к равенству 3 2 х 4 2 = 5 2 , следовательно, он является прямоугольным. Подводя итог, надо отметить, что египетский треугольник, свойства которого уже в течение многих столетий известны человечеству, на сегодняшний день продолжает использоваться в архитектуре. Это вовсе неудивительно, ведь такой способ гарантирует точность, которая очень важна при строительстве. Кроме этого, он очень прост в использовании, что тоже значительно облегчает процесс. Все преимущества использования этого метода прошли проверку веками и остаются популярными до сих пор.
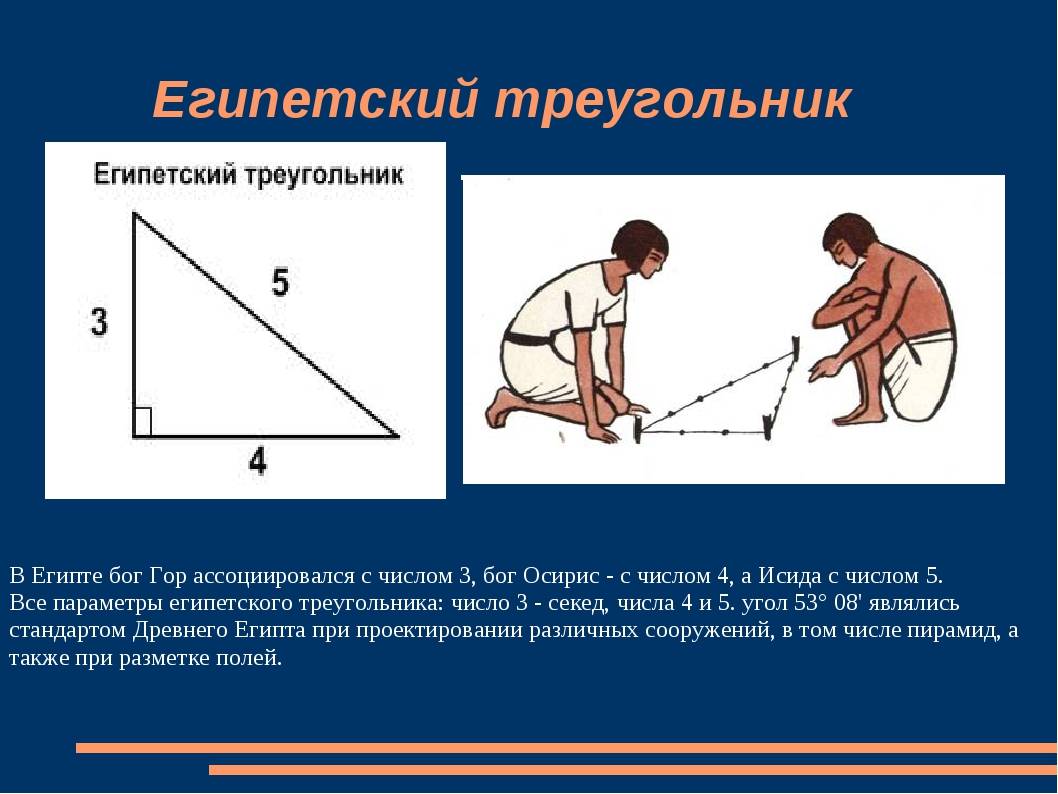
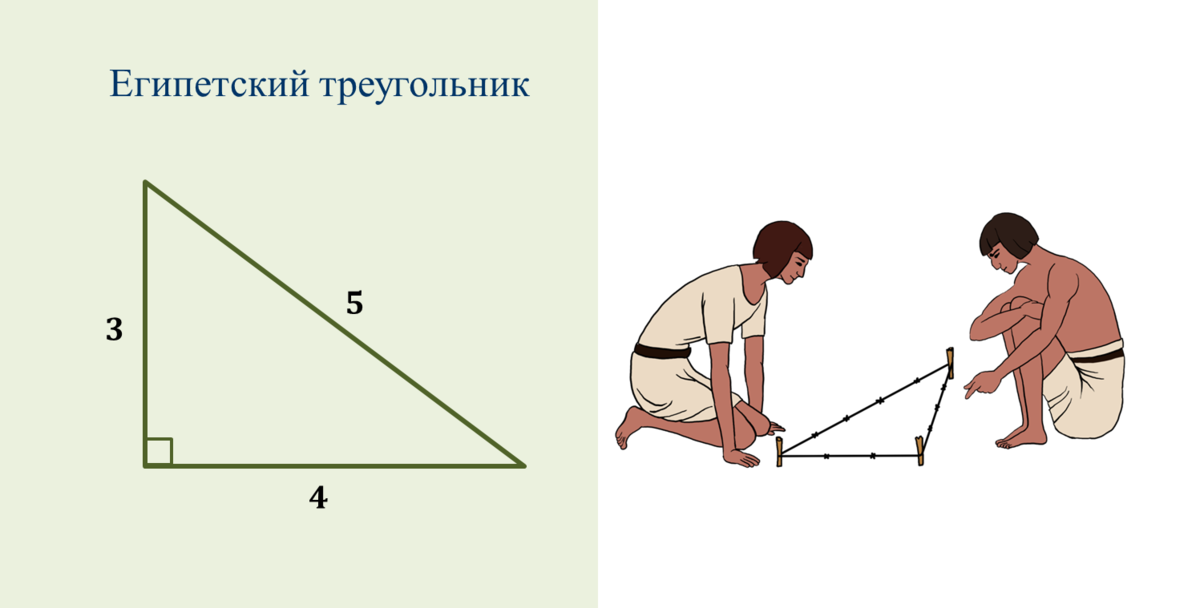
У каждой науки есть свой фундамент, на основании которого и строится все последующее ее развитие. В это, безусловно, теорема Пифагора. Со школьной скамьи учат формулировке: «Пифагоровы штаны во все стороны равны». По научному звучит немного , менее красноречиво. Наглядно эта теорема представляется в со сторонами 3-4-5. Это и есть замечательный Египетский треугольник.
Что такое «египетский треугольник», и откуда он появился
Придумали подобный способ замеров не древние египтяне, как могло бы показаться, судя по названию. На самом деле таким методом разметки пользовались строители ещё задолго до появления пирамид. Суть метода заключается в том, чтобы разделить квадрат будущего строения на два одинаковых треугольника со сторонами, относящимися друг к другу как 3:4:5.
 ФОТО: illvid.dkСтроители в древнем Египте точно знали толк в идеальных сооружениях – их пирамиды стоят до сих пор
ФОТО: illvid.dkСтроители в древнем Египте точно знали толк в идеальных сооружениях – их пирамиды стоят до сих пор
Это должен быть прямоугольный треугольник, подчиняющийся теореме Пифагора. Наверняка все помнят её из школьной программы – сумма квадратов катета равна квадрату гипотенузы, и наоборот. Логически при совмещении этих треугольников должен получиться квадрат с идеально одинаковыми диагоналями. И вот тут начинается самое интересное.
 ФОТО: prezentacii.infoТеорема Пифагора, наверное, самая запоминающаяся из школьного курса – она имеет около 300 доказательств
ФОТО: prezentacii.infoТеорема Пифагора, наверное, самая запоминающаяся из школьного курса – она имеет около 300 доказательств
История символа Трикветр

Блокнот с кельтским трилистником дарит силы и вдохновение для творчества Начало истории Трикветра относят к 4-6 векам н.э. Изображение знака нашли на рунических камнях Скандинавии (валуны с символическими образами). Знак больше всего связан с древними кельтами, поскольку он изображен на кельтских крестах. В Средневековье он появляется у древних славян. Народы Центральной и Северной Европы используют его в ритуальных практиках и магических обрядах.
Разные народы использовали древний знак по-разному:
- рисовали на горшках и орудиях быта;
- использовали для отсчета лунных фаз;
- наносили знак на монеты;
- вырезали на пряжках и ремнях;
- изображали у входа в жилище.
По поверью, у славян считалось, что «Рыба Иешуа» способна сохранить дом, спасти семейный очаг от бед, создать более прочные отношения в браке. Знак в славянской мифологии символизировал домашний очаг, семью, брак. Его изображение, вплетенное в народные мотивы, носило название «славянский орнамент».

Создание этого амулета под силу русским мастеровым-умельцам
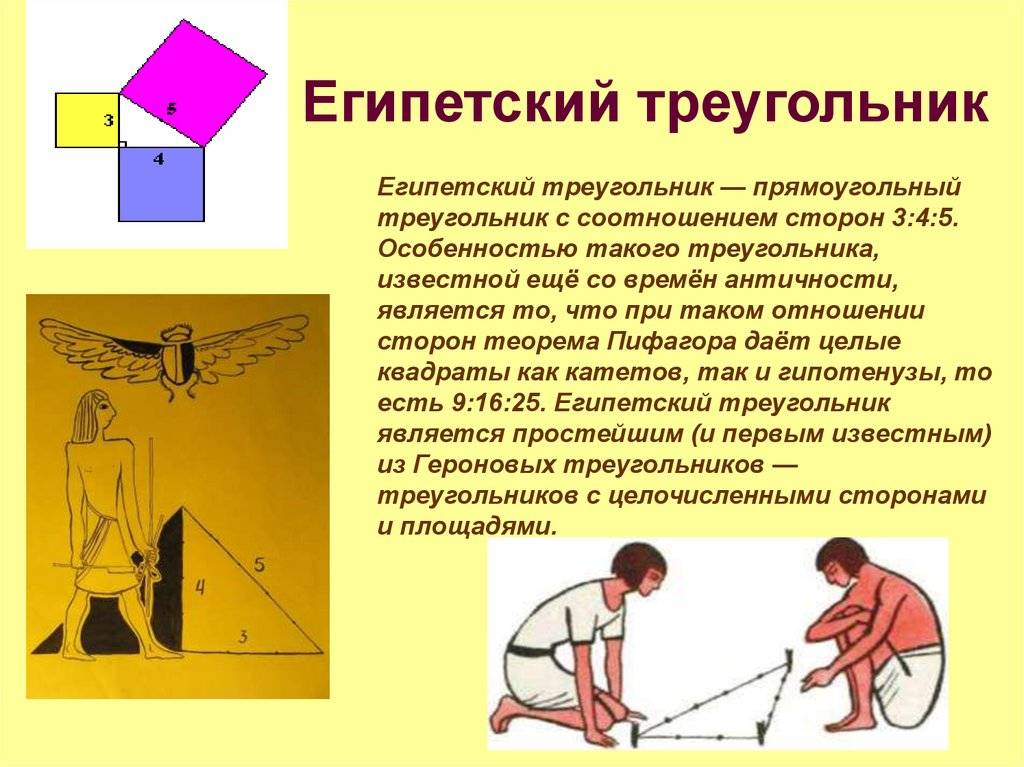
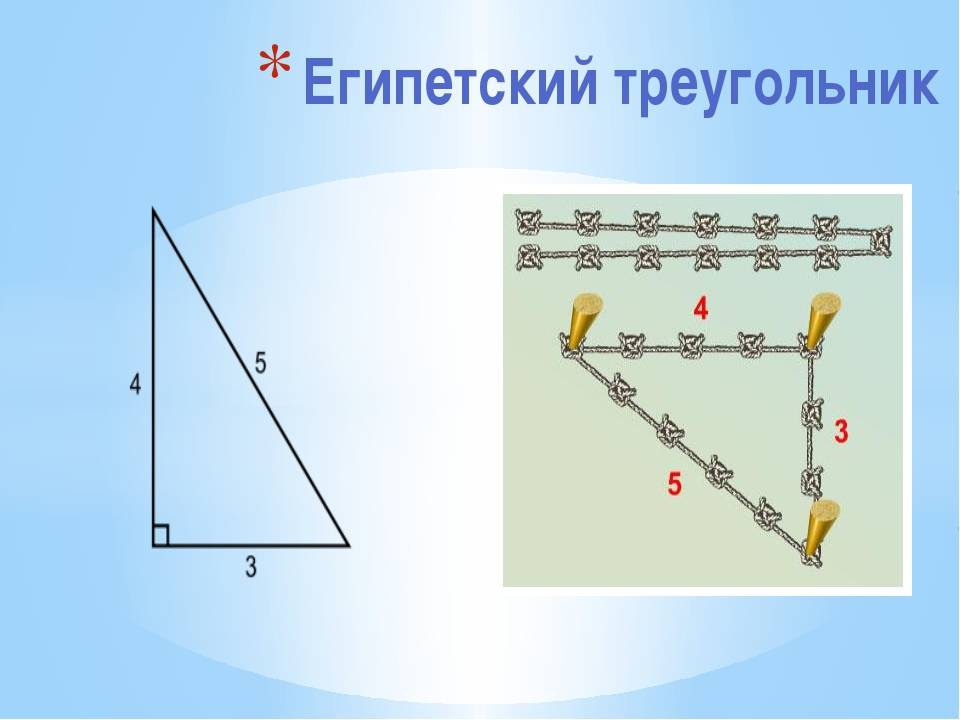
Египетский треугольник
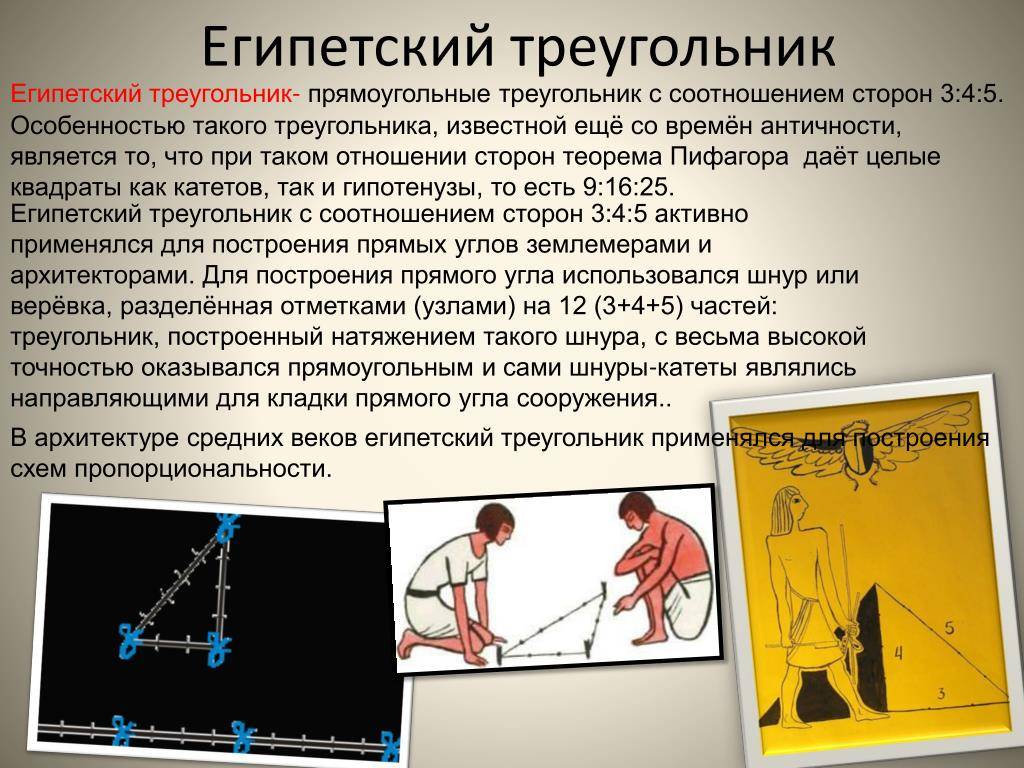
О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.
История египетского треугольника
Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.
Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.

Египетский треугольник в строительстве
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.
Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Альтернативные способы построить прямой угол на 90 градусов
Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.
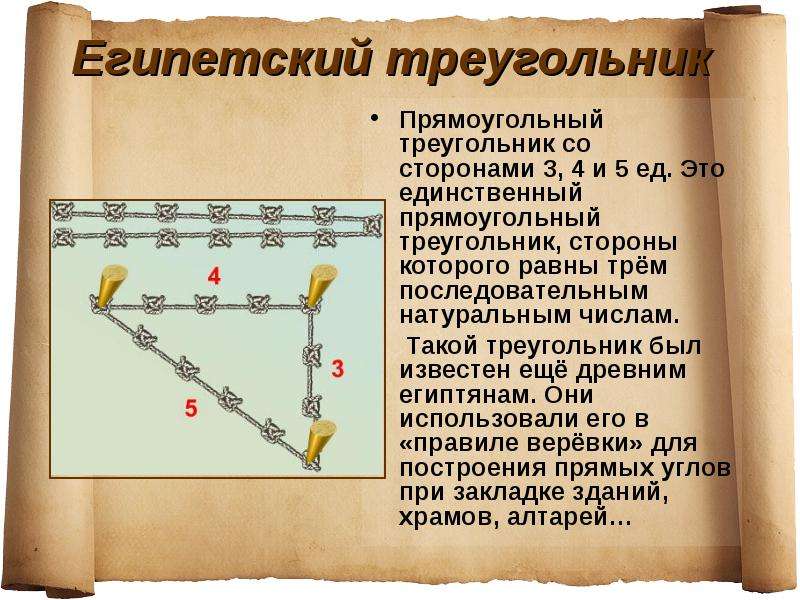
Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.
Как построить угол в 45, 30 и 60 градусов
Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.
Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.
Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.
История открытия
Название египетский треугольник получил благодаря эллинам и Пифагору, которые были частыми гостями в Египте. И случилось это приблизительно в VII-V веках до н. э.
Знаменитая пирамида Хеопса, вообще-то представляет собой прямоугольный многоугольник, а вот священным египетским треугольником принято считать пирамиду
Хефрена.
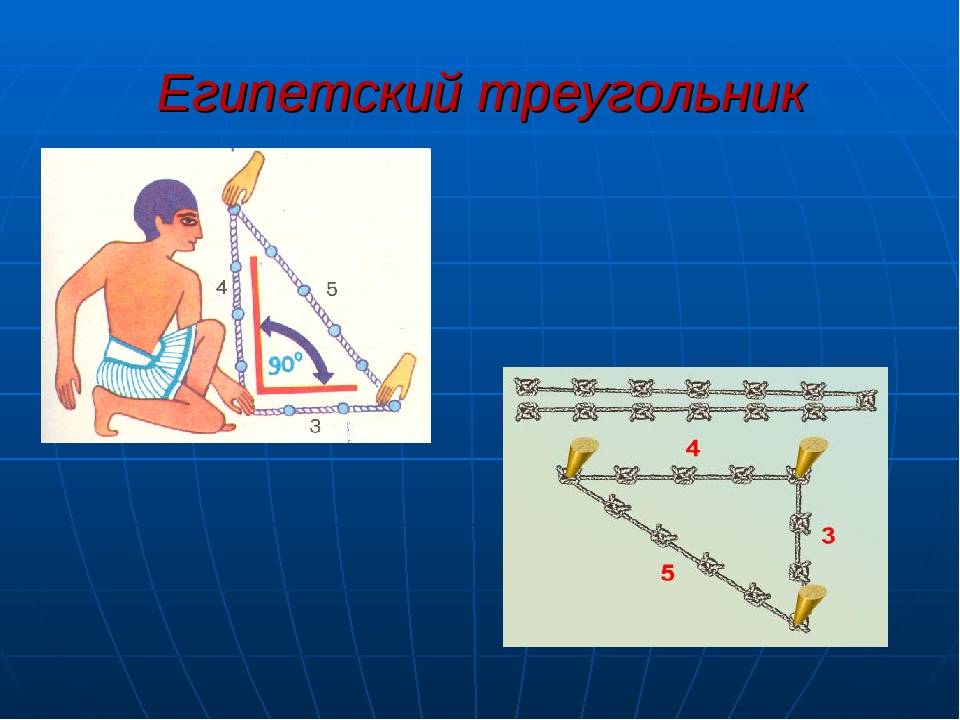
Жители Египта природу Египетского треугольника, как писал Плутарх, сопоставляли с семейным очагом. В их трактовках можно было услышать, что в этой геометрической фигуре ее вертикальный катет символизировал мужчину, основание фигуры относилось к женскому началу, а гипотенузе пирамиды отводилась роль ребенка.
А уже из изученной темы вам хорошо известно, что соотношение сторон этой фигуры равно 3:4:5 и, следовательно, что это нас приводит к теореме Пифагора, так как 32 + 42= 52.
И если учесть, что в основании пирамиды Хефрена лежит египетский треугольник, то можно сделать вывод, народ древнего мира знал знаменитую теорему еще задолго до того, как она была сформулирована Пифагором.
Основной особенностью египетского треугольника, скорее всего, было его своеобразное соотношение сторон, которое было первым и простейшим из Героновых треугольников, так как и стороны, и его площадь имели целые числа.
Небольшие хитрости
Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?
Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.
Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.
Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.
Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом , так как режутся они с правильными углами.
Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.
О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.
2а. ПРАВИЛА ПРИЕМКИ
2а.1. Для проверки соответствия угольников требованиям настоящего стандарта предприятие-изготовитель должно проводить приемочный контроль, периодические испытания и испытания на надежность.
(Измененная редакция, Изм. № 3).
2а.2. При приемочном контроле каждый угольник проверяют на соответствие требованиям пп. 2.1- 2.7, 2.9- 2.11.
2а.3. Периодические испытания проводят не реже раза в три года. Периодическим испытаниям подвергают не менее трех угольников, из числа прошедших приемочный контроль, на соответствие всем требованиям настоящего стандарта.
При этом показатели п. 2.17 подтверждаются результатами анализа подконтрольной эксплуатации не менее пяти угольников. Результаты анализа подконтрольной эксплуатации считают положительными, если: среднее значение полного срока службы контролируемых угольников не менее 5 лет ( п. 2.17), все контролируемые угольники не достигнут предельного состояния в течение 2,5 лет ( п. 2.17).
Если при испытаниях обнаружено, что угольники соответствуют всем требованиям настоящего стандарта, результаты периодических испытаний считают удовлетворительными.
(Измененная редакция, Изм. № 3, 4).
Египетский треугольник в строительстве
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.
Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника. Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
Стороны конструкции имеют следующее соотношение друг к другу:
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
- 5,
- 4,
- 3.
Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.
Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов. Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять
В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять
Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять
Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.
Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам
Альтернативные способы построить прямой угол на 90 градусов
Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.
Как получить египетский треугольник при помощи верёвки
Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.
Как построить угол в 45, 30 и 60 градусов
Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.
Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть
Края должны совпасть.
Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.
Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках
Полезно вспомнить
Треугольник
Треугольник
прямолинейный, часть плоскости, ограниченная тремя отрезками прямых (стороны Треугольника (в геометрии)), имеющими попарно по одному общему концу (вершины Треугольника (в геометрии)). Треугольник, у которого длины всех сторон равны, называется равносторонним
, или правильным
, Треугольник с двумя равными сторонами – равнобедренным
. Треугольник называется остроугольным
, если все углы его острые; прямоугольным
– если один из его углов прямой; тупоугольным
– если один из его углов тупой. Более одного прямого или тупого угла Треугольник (в геометрии) иметь не может, так как сумма всех трёх углов равна двум прямым углам (180° или, в радианах, p). Площадь Треугольник (в геометрии) равна ah/2, где а – любая из сторон Треугольника, принимаемая за его основание, a h – соответствующая высота. Стороны Треугольника подчинены условию: длина каждой из них меньше суммы и больше разности длин двух других сторон.
Треугольник
– простейший многоугольник , имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.
- Трём точкам пространства, не лежащим на одной прямой, соответствует одна и только одна плоскость.
- Любой многоугольник можно разбить на треугольники – этот процесс называется триангуляция
. - Существует раздел математики, целиком посвящённый изучению закономерностей треугольников – Тригонометрия
.
Типы треугольников
По виду углов
Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:
- Если все углы треугольника острые, то треугольник называется остроугольным;
- Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
- Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
По числу равных сторон
- Разносторонним называется треугольник, у которого длины трёх сторон попарно различны.
- Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
- Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.
Кнопки, которые могут отображаться на листе
Рядом с ячейками отображаются семь кнопок: Параметры автозамены
,Параметры вставки , параметры автозаполнения,Ошибка трассировки ,Параметры вставки иприменение правила форматирования .
Параметры автозамены
При наведении указателя мыши на маленькую синюю рамку в разделе текст, который был автоматически исправлен, может появиться кнопка Параметры автозамены
. Например, если ввести в ячейку гиперссылку или адрес электронной почты, может появиться кнопкаПараметры автозамены . Если вы нашли текст, который вы не хотите исправлять, вы можете отменить исправление или включить или отключить параметры автозамены. Чтобы включить или отключить параметры автозамены, нажмите кнопкуПараметры автозамены и выберите нужный вариант из списка.
Египетский треугольник в строительстве. Общие сведения
Зарождение идеи
Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.
Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.
Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.
Из истории
Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.
Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.
Строение
Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.
Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.
Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?
Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.
Обратное доказательство
Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32х42=52 и значит он действительно прямоугольный.
Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».
Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.
Особенности
Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:
- все стороны и площадь состоят из целых чисел, как говорилось выше;
- согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
- такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
- не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.
Что такое угольник и для чего он предназначен
Угольником называется измерительный инструмент, состоящий из двух линеек, расположенных под углом 90 градусов друг к другу. Применяется он в различных сферах — в строительстве, в слесарном и столярном деле, на производстве и т.п. Главное предназначение этого устройства заключается в нанесении прямых линий, расположенных перпендикулярно друг к другу.
Угольник еще называют поверочным, так как с его помощью осуществляется проверка конструкций на наличие брака. Многие используют этот инструмент только для начертания прямых линий под углом 90 градусов, и даже не догадываются о том, что прибором также можно начертить линию с любым другим наклоном.

Главное достоинство рассматриваемого инструмента в том, что он имеет простую конструкцию. Это отражается не только на его стоимости, но и возможности изготовления своими руками. Чтобы сделать угольник, понадобится соединить две линейки, расположив их перпендикулярно друг к другу. Посредством полученного устройства можно наносить не только перпендикулярные линии, но и параллельные.
Это интересно!Угольник — это главный инструмент плотников, строителей и каменщиков, так как с его помощью осуществляется быстрое и точное измерение прямого угла.
Иные способы выведения прямого угла
Если нет желания заниматься выведением углов самостоятельно, а финансы позволяют обратиться за помощью к специалистам, можно вообще не думать об этом вопросе. Один звонок − и на участке уже находится геодезист с теоделитом, который в сжатые сроки сделает разметку. Однако в этом случае необходимо быть готовым к внушительным затратам на оплату его труда.
 ФОТО: omegagalvanoplastia.com.brТеоделит – высокоточная техника, однако стоимость подобной разметки может влететь «в копеечку»
ФОТО: omegagalvanoplastia.com.brТеоделит – высокоточная техника, однако стоимость подобной разметки может влететь «в копеечку»
Если говорить о минимальных затратах, то, основываясь на прайс-листах фирм, оказывающих подобные услуги, вызов и работа геодезиста с инструментом обойдётся в 1 000 руб./час при минимальной оплате 7 000 руб. Дальше − больше. Разметка осей (2 точки) – ещё 3 000 рублей. Если же потребуется определить точные координаты по GPS, то здесь каждые три точки обойдутся владельцу в 5 000 руб. Можно посчитать, какова будет общая сумма (все цены указаны с учётом на конец сентября 2020 года). Не проще ли самому произвести все необходимые разметки? Ведь сэкономленные средства всегда можно потратить на что-то полезное в дальнейшем строительстве.
 ФОТО: thelundreport.orgСтоит приготовиться к тому, что карман значительно облегчится
ФОТО: thelundreport.orgСтоит приготовиться к тому, что карман значительно облегчится
Заключительное слово
Что бы ни говорили противники описанного метода измерений, но «египетский треугольник» в значительной степени помогает строителям в выведении прямых углов. Конечно, при условии его правильного использования. Тем более что навязать 12 узлов на верёвке на определённом расстоянии один от другого много времени не потребует. Также это не потребует и финансовых затрат, связанных с наймом геодезиста с необходимым оборудованием.
 ФОТО: profipol.dp.uaТак должны быть расположены узлы на верёвке для построения «египетского треугольника»
ФОТО: profipol.dp.uaТак должны быть расположены узлы на верёвке для построения «египетского треугольника»
 Watch this video on YouTube
Watch this video on YouTube
Предыдущая DIY HomiusПрочные хомуты из ПЭТ-бутылки за минуту
Следующая DIY HomiusСмеяться или плакать: ошибки во время ремонта